Probabilistic hypothesis testing

2025-12-13

We have a coin, with $p - \text{probability of 1 (head)}$ and $(1 - p) - \text{probability of 0 (tail)}$. We tossed it $n$ times and got a results: $n: x_1, x_2, \dots, x_n \in \{0, 1\}$. Our task it will be a checking the truth of hypothesis $H_0: p = 0.5$. If $H_0$ will be false, we need to choose alternative hypothesis $H_1: p \neq 0.5$.

Firstly, let’s make a little speculations, using our intuition. We, sure, if $\sum\limits_{i = 1}^{n}{x_i} = n$, that $H_0$ is false, because we haven’t reason for assume, that coin can be $0$, therefore $p = 1$. But, what about case, when we have $n = 20$ and $\sum{x_i} = 15$? In this case, we can’t be sure. Our questions, it’s, how to make a decision in such situations. In this decision we may make a one of two types of errors:

And in statistics our default predisposition it’s minimization errors of type 1. For example, if we made a medicine drug and after testing we checking $H_0$: “Our medicine drug is effective.”. If we make error of type 1, we will put broken drug to many peoples — it’s not good. In business, if make first type error we need to spend more many for new model. That’s the reason, for:

For make this decision we need to compare $\sum{x_i}$ with $0.5n$. How big is difference? The theorem of Moivre–Laplace:

Let’s use it in our case:

For example, if in real experiment we got $Z = 10$, that’s mean $H_0$ is very unlikely. So, we need to define the border $t$ for $Z$, after that we reject $H_0$: 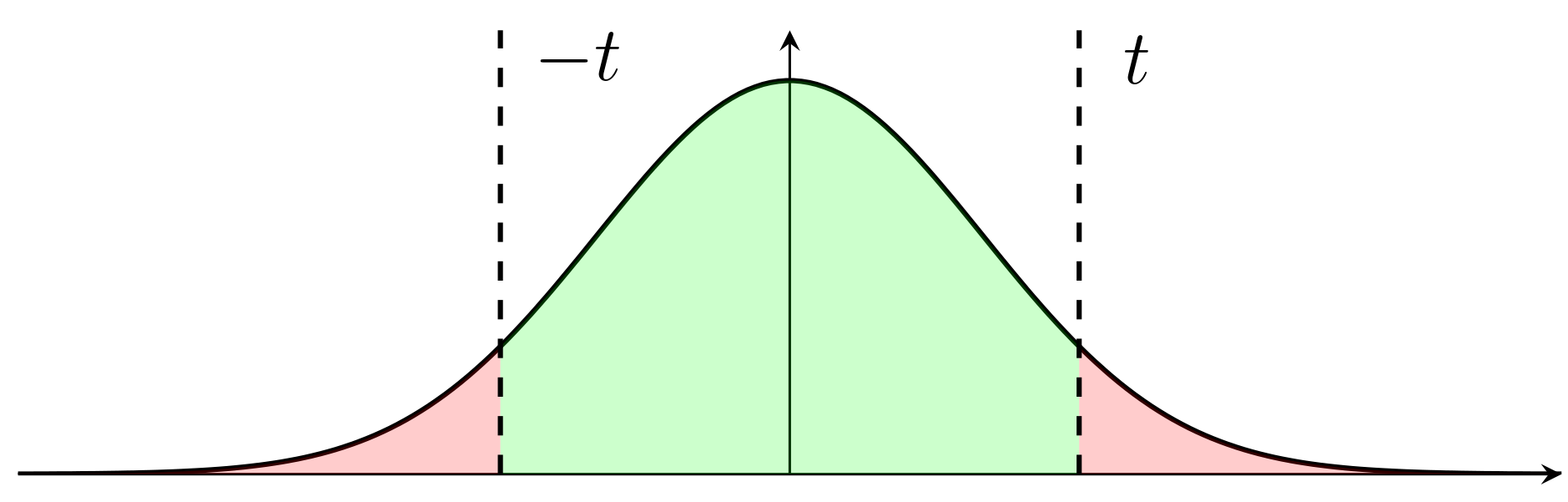We need to find the value of $t$, that probability of cross over it, is significance level $\alpha$. If $|Z| > q_{1 - \frac{\alpha}{2}}$, we talk $H_1$ is truth and we reject $H_0$. Else, we approve $H_0$.

The interesting fact is first type of errors very easy for control. We can always say, that $H_0$ is truth. Then probability of errors type 1 will equal zero.